 Haskell Hero
Haskell Hero
Interaktivní učebnice pro začínající Haskellisty
|
|
FunkceFunkce jako krabičkaFunkci v krabičkovém modelu znázorňujeme krabičkou. Přesněji krabičkou, do které něco vhodíme, zatřepeme a ono z ní něco vypadne.
Mějme třeba funkci 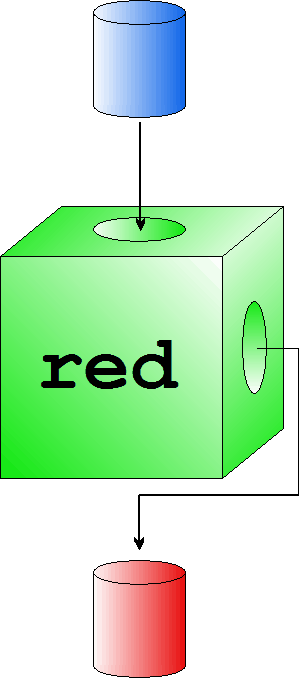 Znázornění funkce red
My budeme pracovat s funkcemi, které zpracovávají nejčastěji čísla nebo seznamy. Například funkci 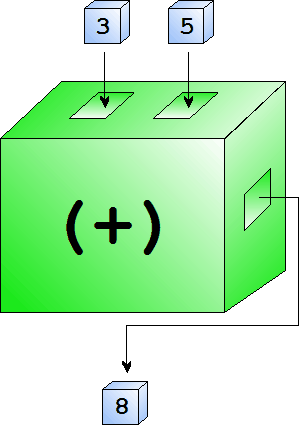 Znázornění funkce (+)
Definice vlastní funkceZákladem funkcionálního programování jsou definice vlastních funkcí. Definice funkce má dvě části, levou a pravou, odděleny znakem rovnítka.
Příklad:
Definujte funkci plus3 5 1 2 ~> 5 + 1 + 2 ~>* 8 Její definice by mohla vypadat následovně: plus3 x y z = x + y + z Příklad:Definujte funkciobvodObdelnika, které dáme délky stran obdélníka a ona vrátí jeho obvod. Aplikace na délky stran například 5 a 3 by měla vypadat následovně:
obvodObdelnika 5 3 ~> 2 * (5 + 3) ~>* 16
Po zaměnění skutečných parametrů obvodObdelnika a b = 2 * (a + b) Definice podle vzoruPříklad:
Definujme funkci
Jedna možnost, jak ji zadefinovat by byla následující: cisloSlovem x = if x == 1 then "Jednicka" else if x == 2 then "Dva" else "Neznam"
Jak bude Hugs postupovat při vyhodnocování výrazu if 2 == 1 then "Jednicka" else if 2 == 2 then "Dva" else "Neznam"Poté vyhodnotí podmínku 2 == 1 na False, takže celý výraz vyhodnotí na else větev vnější podmínky:
if 2 == 2 then "Dva" else "Neznam"Výraz 2 == 2 se vyhodnotí na True, takže se celý výraz vyhodnotí na řetězec "Dva".
Druhou možností je definovat funkci podle vzoru. Ta stejná funkce bude definována podle vzoru následovně. Jednotlivé řádky definice se nazývají klauzule. cisloSlovem 1 = "Jednicka" cisloSlovem 2 = "Dvojka" cisloSlovem x = "Neznam"
Hugs bude v tomto případě při vyhodnocování výrazu
Jak by se vyhodnotil výraz
Jelikož není proměnná cisloSlovem 1 = "Jednicka" cisloSlovem 2 = "Dvojka" cisloSlovem _ = "Neznam" Hugsu při vyhodnocování nezáleží na pořadí definic funkcí ve skriptu. To znamená, že pokud do skriptu napíšeme krat 0 _ = 0 krat x y = plus y (krat (x - 1) y) plus x y = x + yvrátí nám aplikace krat 3 2 správně vypočítaný součin nezáporného čísla 3 a celého čísla 2, což je 6. Pozor ale na pořadí klauzulí! Jak jsme si řekli výše, Hugs při vyhodnocování funkce postupně zkouší, zda se dá použít první klauzule, druhá klauzule, ... Pokud bychom klauzule definice funkce krat prohodili
krat x y = plus y (krat (x - 1) y) krat 0 _ = 0výpočet by nikdy neskončil, neboť by se stále vyhodnocovalo podle první klauzule a docházelo by ke stále většímu rekurzivnímu zanoření. Rekurzivní definicePříklad:
Definujte funkci soucet 3 ~>* 3 + 2 + 1 ~>* 6
Se znalostí definice podle vzoru můžeme funkci soucet 1 = 1 soucet 2 = 2 + 1 soucet 3 = 3 + 2 + 1 soucet 4 = 4 + 3 + 2 + 1 soucet 5 = 5 + 4 + 3 + 2 + 1
My ale potřebujeme obecnou definici, která by umožnila výpočet funkce Pěkné znázornění, co to rekurze je, můžete najít na české necyklopedii. Stručně řečeno, rekurzivní funkce je funkce, která se vyhodnotí na výraz obsahující sebe samu.
Pokud se podíváme na definici soucet 1 = 1 soucet 2 = 2 + soucet 1 soucet 3 = 3 + soucet 2 soucet 4 = 4 + soucet 3 soucet 5 = 5 + soucet 4
Z tohoto zápisu už můžeme odvodit obecný zápis funkce soucet x = x + soucet (x - 1)
Pokud si ale necháme vyhodnotit výraz soucet 3 ~> 3 + soucet 2 ~> 3 + 2 + soucet 1V tomto místě bychom chtěli, aby se výpočet zastavil. On ale podle definice bude pokračovat dále: ~> 3 + 2 + 1 + soucet 0 ~> 3 + 2 + 1 + 0 + soucet (-1) ~> 3 + 2 + 1 + 0 + (-1) + soucet (-2) ~> ...Proto musíme k definici přidat zastavující klauzuli, která výraz soucet 1 nahradí výrazem 1 a tím ukončí rekurzivní volání. Správná definice funkce soucet by tedy vypadala následovně:
soucet 1 = 1 soucet x = x + soucet (x - 1) PoznámkaJelikož je rekurze ve funkcionálním programování hojně využívaným prvkem, již existuje velké množství knihoven s funkcemi, které rekurzi řeší za nás. Z těchto většinou jednoduchých funkcí pak můžeme skládat funkce složitější. Lokální definiceUž víme, jak definovat vlastní funkci. Jak ale říct její definici Hugsu? Máme dvě možnosti. Můžeme ji definovat buďto lokálně, nebo globálně. V tomto odstavci se podíváme na lokální definici. Lokální definice se zapisuje jako v tomto tvaru: let definice in výrazkde se místo definice napíše definice funkce nebo konstanty a místo výraz se napíše výraz, který se následně vyhodnotí za použití definice v části definice. Definici se říká lokální, protože je platná pouze v části výraz příslušného let-výrazu.
Příklady:
let pet = 5 in 5 + pet ~> 5 + 5 ~> 10
let plus3 x y z = x + y + z in plus3 1 3 5
~> 1 + 3 + 5 ~>* 9
Pokud potřebujeme definovat více než jednu funkci nebo konstantu v jednom
let {dva = 2; tri = 3; pet = 5; plus3 x y z = x + y + z}
in plus3 tri pet dva
~> 3 + 5 + 2 ~>* 10
Druhá varianta lokální definice je lokální definice s výraz where definicea chová se úplně stejně, jako let-výraz.
Příklad:
plus3 1 3 5 where plus3 x y z = x + y + z |