Haskell Hero

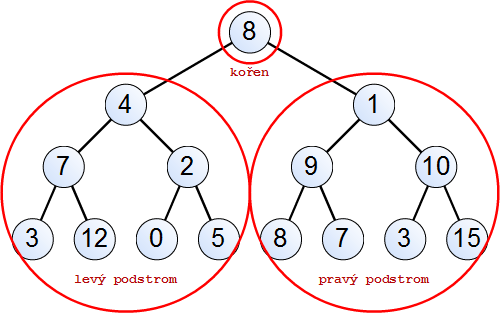Binární strom

Binární strom je datová struktura. Může být buďto prázdný nebo neprázdný. Neprázdný strom se skládá z

• kořene a hodnoty v kořeni
• levého podstromu
• pravého podstromu

V Haskellu jej budeme definovat následovně:

data BinTree a  =  Empty  |  Node a (BinTree a) (BinTree a)

Node a (BinTree a) (BinTree a)

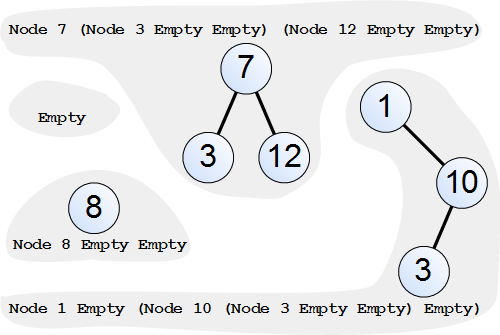Ukázky binárních stromů typu BinTree Int

Příklad

Definujte funkci size :: BinTree a -> Int, kde výraz size tree se vyhodnotí na počet uzlů stromu tree.

Jak začít? Drtivá většina funkcí na binárních stromech vypadá následovně:

• Pokud je strom prázdný, vyhodnoť se na určitou hodnotu.
• Pokud je strom neprázdný, aplikuj funkci rekurzivně na levý a pravý podstrom. Z těchto výsledků a z hodnoty kořene poskládej výsledek, na který se vyhodnoť.

Můžeme si tedy nadepsat definici:

size              ::  BinTree a  ->  Int
size Empty         =
size (Node x l r)  =

Kolik uzlů je v prázdném stromě? Přesně nula. Můžeme tedy doplnit první klauzuli.

size Empty  =  0

Kolik uzlů je v neprázdném stromě? Na tuto otázku už není možné odpovědět tak rychle, jako na předchozí. Podívejme se, co máme k dispozici. Je to hodnota v kořeni, levý podstrom a pravý podstrom. Nic víc.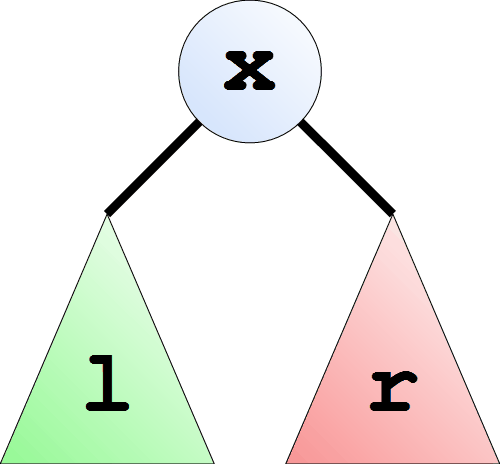

Kolik je uzlů v takovém stromě? Přesně tolik, kolik je dohromady v levém podstromu, v pravém podstromu a v kořeni. Čili rekurzivně spočítáme uzly v levém podstromu, spočítáme uzly v pravém podstromu a přičteme jedničku za uzel v kořeni. A přesně tak to zapíšeme.

size (Node x l r)  =  size l  +  size r  +  1

size              ::  BinTree a  ->  Int
size Empty         =  0
size (Node _ l r)  =  size l  +  size r  +  1

Vzorové vyhodnocení

Ukážeme si, jak vypadá počítání uzlů tříuzlového stromu.

size (Node 5                  -- x
        (Node 2 Empty Empty)  -- l
        (Node 4 Empty Empty)  -- r
      )

~>  size (Node 2 Empty Empty) + size (Node 4 Empty Empty) +  1

~>  size Empty + size Empty + 1 + size (Node 4 Empty Empty) +  1

~>       0     + size Empty + 1 + size (Node 4 Empty Empty) +  1

~>       0     +      0     + 1 + size (Node 4 Empty Empty) +  1

~>  0 + 0 + 1 + size Empty + size Empty + 1 +  1

~>  0 + 0 + 1 +      0     + size Empty + 1 +  1

~>  0 + 0 + 1 +      0     +      0     + 1 +  1

~>* 3

Kromě binárních stromů můžeme definovat i stromy n-ární. Od binárních stromů se liší tím, že každý uzel může mít libovolný počet následníků. Tvar n-árního stromu má například běžná adresářová struktura.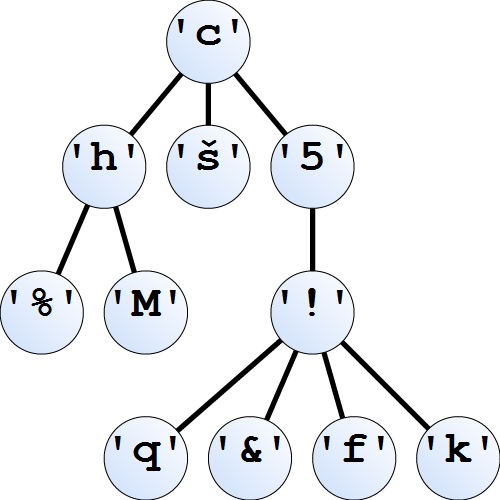

Ukázka n-árního stromu typu NTree Char

V Haskellu budeme n-ární stromy definovat následovně:

data NTree a  =  Nnode a [ NTree a ]

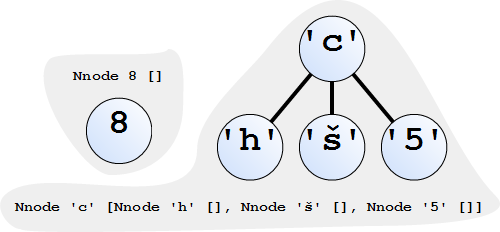Příklady n-árních stromů

Všimněme si, že nemáme definován prázdný strom. Pokud bychom jej měli, tento zápis by vedl k nejednoznačnosti zápisu jednotlivých stromů. Například jednouzlový strom by mohl být definován následně:

data NTree a  =  Empty  |  Nnode a [ NTree a ]

Nnode 3 []
Nnode 3 [Empty]
Nnode 3 [Empty, Empty]
Nnode 3 [Empty, Empty, Empty]
Nnode 3 [Empty, Empty, Empty, Empty]
...

Příklad

Definujte funkci treeSum :: NTree Integer -> Integer, která sečte hodnoty všech uzlů v n-árním stromě.

Když se podíváme, jak n-ární strom vypadá, logicky nám vyplyne následující postup:

• rekurzivně sečteme hodnoty ve všech podstromech
• sečteme tyto spočítané hodnoty dohromady
• k výsledku přičteme hodnotu kořene

K rekurzivnímu sečtení všech stromů v seznamu podstromů použijeme funkci map, k sečtení těchto hodnot použijeme funkci sum. A pak už jen přičteme hodnotu v kořeni.

treeSum             ::  NTree Integer -> Integer
treeSum (Nnode x s)  =  sum (map treeSum s)  +  x

Vzorové vyhodnocení

treeSum (Nnode 5 [
             Nnode 4 [],
             Nnode 6 [],
             Nnode 8 []
         ])

~>   sum (map treeSum [ Nnode 4 [], Nnode 6 [], Nnode 8 [] ]) + 5

~>*  sum              [      4    ,      6    ,      8     ]  + 5

~>*                             18                            + 5

~>   23